Honour Chemistry Semester Break Reading Assignment

We will be embarking on Atomic Orbitals, Chemical Periodicity, Bonding and Structures when we return from the break. Hence, it is very important that you read ahead to get an idea of what’s coming. Look over the math examples but don’t fret them if you don’t understand. Try to comprehend the main ideas by following the development of atomic and quantum science in the early part of the 20^th century. Do this over several days (that means no cramming it all in the night before we get back to school – this is not your typical summer reading assignment for your English class). Enjoy the process of discovery and learning as you try to digest these concepts.

1.  Go through each point below and take in the main idea. Then, read the prescribed section (s) from the textbook (ignore Diamagnetism, Paramagnetism and Shielding Effect in Many-Electron Atoms on pg. 228 & 229). Go to the suggested websites as you focus on the following ideas,.

a.  Light was thought of as waves for the longest time (the shorter the wavelength, the higher the frequency because c = f λ), as it has wave properties like reflection, refraction, and diffraction with interference pattern. The higher the frequency or the shorter the wavelength, the stronger is the light energy, E = hf or E = hc/λ. Read 7.1 of the textbook (pg. 207 to 210).

b.  Planck hypothesized the quantum nature of light (discrete amount of energy) and Einstein later proved by his Photoelectric Experiment. Read 7.2 of the textbook (pg. 211 and 212). A photoelectric device is basically an early version of a solar panel – play with this applet by increasing and decreasing wavelength and intensity of light. This experiment demonstrated that light can behave like a particle (photon) as well as a wave (Einstein won the Noble Prize of Physics for this work). It led to the idea of Wave-Particle Duality of Light.

c.  Bohr used Rutherford’s earlier work of the nuclear model, applied the idea from Planck that light is quantized (discrete in amounts of energy), and that electrons can only exist at specific energy levels. Using mathematical proofs, he developed the Bohr Atomic Model. The model explains how electrons can absorb quantized amounts of energy. As these electrons relax back to their lower energy levels, they give out lights of specific wavelengths – emission spectrum. Since different elements have different number of electrons, their spectrums are as different as fingerprints. Read 7.3 of the textbook (pg. 212 to 217). Look over the calculations in the examples (don’t worry; you won’t have to do them on a test. But you must appreciate how the Bohr Model can mathematically predict these energy levels of a hydrogen atom.) - See this video and view this animation. The Bohr Model is also called as the Shell or Energy Level Model. It has a limitation in that it only work on hydrogen atoms, and there are other problems the Bohr Model cannot explain. Most scientists now classified the Bohr Model as the “old quantum theory”.

d.  de Broglie suggested that matter can have wave properties (since wave can behave like particles as Einstein had proved earlier). He developed an idea an electron is not just a particle, but can also be viewed as waves (see the first 3 ½ minutes of this video). Further evidence provided by George Thomson (J. J Thomson’s son of the Plum Pudding Model fame) using high energy electrons to “see” the diffraction pattern of a crystal – precursor of the modern day electron microscope (see the X-ray Diffraction picture of a DNA molecule by Rosalind Franklin – independent discoverer of DNA – she did not work with Crick and Watson). This generalized into the Particle-Wave Duality of Electrons. The equation [ λ = h/(mv) ] allows us to calculate the wavelength of an electron moving at any velocity. Read 7.4 of the textbook (pg. 217 to 219).

e.  Bohr understood that his shell model was incomplete and fairly limited. Therefore, he decided to work with Heisenberg who realized that electrons could not be observed directly due to its extremely small size. More importantly, the “act” of observing would inevitably change its position (because you would have to shine a light with high frequency to “see” an electron, and it would unavoidably absorb this energy and move to a higher energy level). Hence, there would always be uncertainties associate with the position and momentum of an electron at any given time. This concept is called the Heisenberg Uncertainty Principle. Therefore, atomic orbitals must be thought of as probability clouds where electrons are “likely” to be found. (See PowerPoint slides for more explanation and watch this excellent demo.)

f.   Since electrons in different energy levels can now be thought of as wave according to de Broglie, and not particles, Schrödinger used a complex mathematical model to express these waves as a standing wave functions (sort of like a sinusoidal wave you learned in Algebra 2, except this is in 3-D) Watch this video of standing waves in a ring. (The audio is in Chinese but read the English caption on the video.) Bohr and Heisenberg took Schrödinger wave functions and applied them with their matrix based probability model and developed the Probability Cloud (Density) Model. Read 7.5 of the textbook (pg. 219 to 220). The solutions of these wave functions (or wave equations) are called the Quantum Numbers. These quantum numbers allow us to generate different cloud shapes and sizes (1s, 2s, 2p, 3s, 3p, 3d … etc). They are called Atomic Orbitals.

• n – Principle Quantum Numbers {n = 1, 2, 3, 4 …}. They represent the energy levels (or different sizes of these orbitals)

• l – Angular Quantum Numbers {l = 0, 1, 2, 3, … , (n − 1)}. They represent the different types or shapes of the orbitals We use the letters (s, p, d… etc.) to represent these numbers.

(l = 0 is s-orbital – sphere);                (l = 1 is p-orbital – dumb bell);          (l = 2 is d-orbital –four-leaf clover)

• m_l – Magnetic Quantum Numbers {−l ≤ m_l ≤ l}. They tell you have many orientations each orbital has.

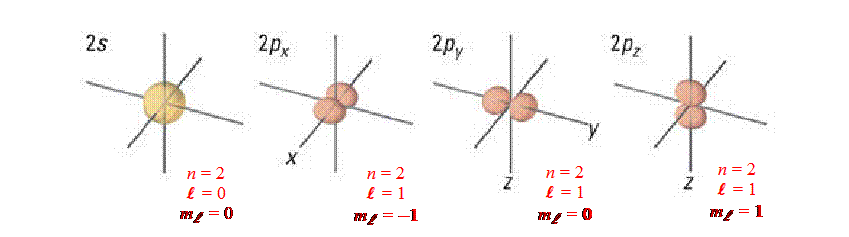
Example: For n = 2, there can be two types of orbitals (l = 0 and l = 1) ® so in energy level n = 2, there are two kinds of orbitals (2s and 2p).

  The s-orbital has 1 orientation (0 ≤ m_l ≤ 0 ® m_l = 0 [one solution means only one orientation for s-orbital]).

  The p-orbital has 2 orientations (−1 ≤ m_l ≤ 1 ® m_l = −1, 0, and 1 [three solutions means only three orientations for p-orbital: p_x, p_y and p_z ]).

Now, Read 7.6 and 7.7 of the textbook (pg. 221 to 226). But if you can’t follow the book, then read the notes on this website. Watch the last 5 ½ minutes of this video.

g.  Pauli (a student / colleague of Heisenberg) understood the spin directions of the electrons can give rise to different magnetic pole directions. Hence, there can only be two electrons in any atomic orbital (see Fig. 7.22b on pg. 228 of textbook). Read the first half of 7.8 of the textbook (pg. 226 to 230).

Break Time: Watch the video clips from the Documentary: “Atom – The Clash of Titans”

h.  Even though Heisenberg and Bohr would say it is impossible to perceive an atom and their orbitals, it would still be nicer to have a conceptual model (a picture if you will). Atomic orbitals can be drawn as Nested Clouds (sort of like those Russian nested dolls - Babushka doll – see diagram below), or they can be drawn as Atomic Orbital Diagrams (slot boxes with arrows), or they can be written out as Electron Configuration. (Please go through the online tutorial: Electron Configurations - Orbital Filling Order. (Use the Table of Elements on pg. 236 of the textbook at the same time.) Also look over this awesome applet. It shows why the 3d orbitals degenerate or move up above the 4s orbital due to electron crowding. This explains why the elements in 3d block of the Periodic Table come after the 4s elements, event though the 3d block is in the 4^th row of the table.

i.   When filling out the atomic orbitals, we have to follow the Aufbau Principle and the Hund’s Rule. Read the last half of 7.8 and 7.9 of the textbook (pg. 230 to 235). Watch this Lecture Video from MIT.

2.  For a recap and summarizing ideas as well as applications using quantum mechanics. Watch all three video clips. Look over the printable flow chart of the development of ideas that lead to the Modern Quantum Mechanics Model. As you can see, it was a collaborative result of many scientists. Remember, don’t get bog down with the details, but understand the main ideas and developments of quantum mechanics view of atoms.

Have a good Break,  Mr. Tang